Paths in Trees
For any two nodes of a tree, a unique path connects the nodes;
more specifically, there is a unique path connecting any pair of leaves.
Why must this be the case? If more than one path connected two nodes, then they would
necessarily form a cycle, which would violate the definition of tree.
The uniqueness of paths connecting nodes in a tree is helpful in phylogenetic analysis
because a rudimentary measure of the separation
between two taxa is the distance between them in the tree, which is equal to the
number of edges on the unique path connecting the two leaves corresponding to the taxa.
Problem
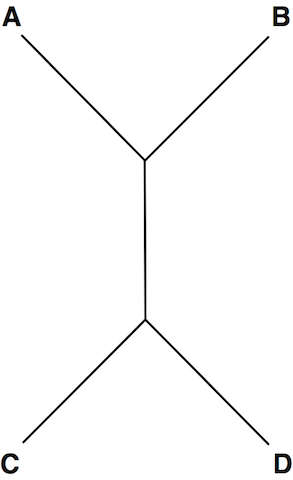
Figure 1. This tree can be represented in Newick format in a number of ways, including (C, D, (A, B)); (A, (D, C), B); and (((A, B), C), D);.
Newick format is a way of representing trees even more concisely than using an adjacency list,
especially when dealing with trees whose internal nodes have not been labeled.
First, consider the case of a rooted tree $T$. A collection of leaves $v_1, v_2, \ldots, v_n$ of $T$ are neighbors if they are all adjacent to some internal
node $u$. Newick format for $T$ is obtained by iterating the following key step: delete all the edges $\{v_i, u\}$
from $T$ and label $u$ with $(v_1, v_2, \ldots, v_n)u$. This process is repeated all the
way to the root, at which point a semicolon signals the end of the tree.
A number of variations of Newick format exist. First, if a node is not labeled in $T$, then we simply leave blank the
space occupied by the node. In the key step, we can write $(v_1, v_2, \ldots, v_n)$ in place of $(v_1, v_2, \ldots, v_n)u$ if the $v_i$
are labeled; if none of the nodes are labeled, we can write $(, , \ldots, )$.
A second variation of Newick format occurs when $T$ is unrooted, in which case we
simply select any internal node to serve as the root of $T$. A particularly peculiar case
of Newick format arises when we choose a leaf to serve as the root.
Note that there will be a large number of different ways to represent $T$ in Newick format;
see Figure 1.
Given: A collection of $n$ trees ($n \leq 40$) in Newick format, with each tree containing at most 200 nodes;
each tree $T_k$ is followed by a pair of nodes $x_k$ and $y_k$ in $T_k$.
Return: A collection of $n$ positive integers, for which the $k$th integer represents the distance
between $x_k$ and $y_k$ in $T_k$.
Sample Dataset
(cat)dog;
dog cat
(dog,cat);
dog cat
Sample Output
