April 5, 2013, 3:30 p.m. by Rosalind Team
Topics: Combinatorics, Dynamic Programming, String Algorithms
The Dirty Truth About Mathematics Parties
In “Catalan Numbers and RNA Secondary Structures”, we talked about counting the number of ways for an even number of people to shake hands at a party without crossing hands. However, in the real world, parties only contain an even number of people about 30% of the time, and mathematicians aren't social butterflies. So we should instead count the total number of ways for some of the people at the party to shake hands without crossing.
In the biological world, people are perhaps more social, but not every nucleotide in a strand of RNA winds up base pairing with another nucleotide during RNA folding. As a result, we want to loosen this assumption and count the total number of different secondary structures of an RNA strand whose base pairs don't overlap (i.e., we still forbid pseudoknots in the strand).

Similarly to our definition of the Catalan numbers,
the
How should we compute the Motzkin numbers? As with Catalan numbers, we will take
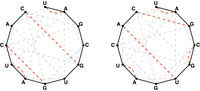
To count all possible secondary structures of a given RNA string that do not contain pseudoknots, we need to modify the Motzkin recurrence so that it counts only matchings of basepair edges in the bonding graph corresponding to the RNA string; see Figure 2.
Given: An RNA string
Return: The total number of noncrossing matchings of basepair edges in the bonding graph
of
>Rosalind_57 AUAU
7