Maximum Matchings and RNA Secondary Structures solved by 1787

Breaking the Bonds

In “Perfect Matchings and RNA Secondary Structures”, we considered a problem that required us to assume that every possible nucleotide is involved in base pairing to induce an RNA secondary structure. Yet the only way this could occur is if the frequency of adenine in our RNA strand is equal to the frequency of uracil and if the same holds for guanine and cytosine.

We will therefore begin to explore ways of counting secondary structures in which this condition is not required. A more general combinatorial problem will ask instead for the total number of secondary structures of a strand having a maximum possible number of base pairs.

Problem

Figure 1. The bonding graph of s = UAGCGUGAUCAC (left) has a perfect matching of basepair edges, but this is not the case for t = CAGCGUGAUCAC (right), in which one symbol has been replaced.

Figure 2. A maximum matching (highlighted in red) is shown in each of the three graphs above. You can verify that no other matching can contain more edges. (Courtesy: Miym, Wikimedia Commons User)

Figure 3. A red maximum matching of basepair edges in the bonding graph for t = CAGCGUGAUCAC.

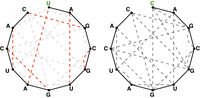
The graph theoretical analogue of the quandary stated in the introduction above is that if we have an RNA string $s$ that does not have the same number of occurrences of 'C' as 'G' and the same number of occurrences of 'A' as 'U', then the bonding graph of $s$ cannot possibly possess a perfect matching among its basepair edges. For example, see Figure 1; in fact, most bonding graphs will not contain a perfect matching.

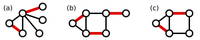
In light of this fact, we define a maximum matching in a graph as a matching containing as many edges as possible. See Figure 2 for three maximum matchings in graphs.

A maximum matching of basepair edges will correspond to a way of forming as many base pairs as possible in an RNA string, as shown in Figure 3.

Given: An RNA string $s$ of length at most 100.

Return: The total possible number of maximum matchings of basepair edges in the bonding graph of $s$.

Sample Dataset

>Rosalind_92
AUGCUUC

Sample Output

6