Mortal Fibonacci Rabbits solved by 13232

Wabbit Season

Figure 1. A c.1905 photo from Australia of a cart loaded to the hilt with rabbit skins.

Figure 2. Western Australia's rabbit fence is actually not the longest fence in the world as the sign claims. That honor goes to a 3,500 mile fence in southeastern Australia built to keep out dingoes. Courtesy Matt Pounsett.

Figure 3. An 1884 cartoon from the Queensland Figaro proposing how the rabbits viewed their fence.

In “Rabbits and Recurrence Relations”, we mentioned the disaster caused by introducing European rabbits into Australia. By the turn of the 20th Century, the situation was so out of control that the creatures could not be killed fast enough to slow their spread (see Figure 1).

The conclusion? Build a fence! The fence, intended to preserve the sanctity of Western Australia, was completed in 1907 after undergoing revisions to push it back as the bunnies pushed their frontier ever westward (see Figure 2). If it sounds like a crazy plan, the Australians at the time seem to have concurred, as shown by the cartoon in Figure 3.

By 1950, Australian rabbits numbered 600 million, causing the government to decide to release a virus (called myxoma) into the wild, which cut down the rabbits until they acquired resistance. In a final Hollywood twist, another experimental rabbit virus escaped in 1991, and some resistance has already been observed.

The bunnies will not be stopped, but they don't live forever, and so in this problem, our aim is to expand Fibonacci's rabbit population model to allow for mortal rabbits.

Problem

Figure 4. A figure illustrating the propagation of Fibonacci's rabbits if they die after three months.

Recall the definition of the Fibonacci numbers from “Rabbits and Recurrence Relations”, which followed the recurrence relation $F_n = F_{n-1} + F_{n-2}$ and assumed that each pair of rabbits reaches maturity in one month and produces a single pair of offspring (one male, one female) each subsequent month.

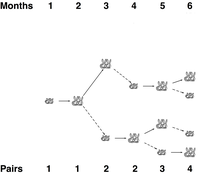
Our aim is to somehow modify this recurrence relation to achieve a dynamic programming solution in the case that all rabbits die out after a fixed number of months. See Figure 4 for a depiction of a rabbit tree in which rabbits live for three months (meaning that they reproduce only twice before dying).

Given: Positive integers $n \leq 100$ and $m \leq 20$.

Return: The total number of pairs of rabbits that will remain after the $n$-th month if all rabbits live for $m$ months.

Sample Dataset

6 3

Sample Output

4