March 16, 2013, 6:22 a.m. by Rosalind Team
Topics: Combinatorics, Dynamic Programming, String Algorithms
The Human Knot
Figure 2. This pseudoknot was formed when bonding occurred at the endpoints of overlapping intervals [1,3] and [2, 4]. (Courtesy: Sakurambo, Wikimedia Commons User)You may have had the misfortune to participate in a team-building event that featured the "human knot," in which everyone joins hands with two other people, and the group must undo the giant knot of arms without letting go (see Figure 1).
Let's consider a simplified version of the human knot. Say that we have an even number of people at a party who are standing in a circle, and they pair off and shake hands at the same time. One combinatorial question at hand asks us to count the total number of ways that the guests can shake hands without any two pairs interfering with each other by crossing arms.
This silly little counting problem is actually an excellent analogy for RNA folding. In practice, base pairing can occur anywhere along the RNA molecule, but the secondary structure of RNA often forbids base pairs crossing over each other, which forms a structure called a pseudoknot (see Figure 2)). Pseudoknots are not technically knots, but they nevertheless cause RNA to fold over itself.
Forbidding pseudoknots offers an interesting wrinkle to the problem of counting potential RNA secondary structures that we started working with in “Perfect Matchings and RNA Secondary Structures”, in which every possible nucleotide of a strand of RNA must base pair with another nucleotide.
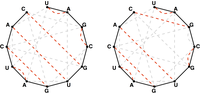

A matching in a graph is noncrossing
if none of its edges cross each other. If we assume that the
A noncrossing matching of basepair edges in the bonding graph corresponding to an RNA string will correspond to a possible secondary structure of the underlying RNA strand that lacks pseudoknots, as shown in Figure 3.
In this problem, we will consider counting noncrossing perfect matchings of basepair edges.
As a motivating example of how to count noncrossing perfect matchings,
let
There are
Given: An RNA string
Return: The total number of noncrossing perfect matchings of basepair edges in the bonding
graph of
>Rosalind_57 AUAU
2
Hint
Write a function that counts Catalan numbers via dynamic programming. How can we modify this function to apply to our given problem?