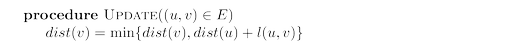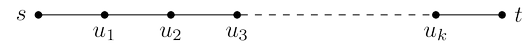Dijkstra's algorithm works in part because the shortest path from the starting point $s$ to any
node $v$ must pass exclusively through nodes that are closer than $v$. This no longer holds when
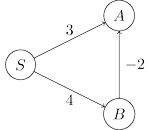
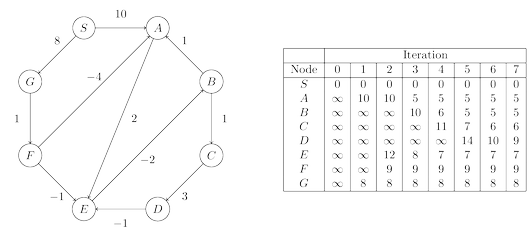
edge lengths can be negative. In figure below, the shortest path from $S$ to $A$ passes through $B$,
a node that is further away!
What needs to be changed in order to accommodate this new complication? To answer this,
let’s take a particular high-level view of Dijkstra’s algorithm. A crucial invariant is that the
$dist$ values it maintains are always either overestimates or exactly correct. They start off at
$\infty$, and the only way they ever change is by updating along an edge:
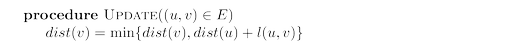
This update operation is simply an expression of the fact that the distance to $v$ cannot possibly
be more than the distance to $u$, plus $l(u, v)$. It has the following properties.
- It gives the correct distance to $v$ in the particular case where $u$ is the second-last node
in the shortest path to $v$, and $dist(u)$ is correctly set.
- It will never make $dist(v)$ too small, and in this sense it is safe. For instance, a slew of
extraneous $\tt update$’s can’t hurt.
This operation is extremely useful: it is harmless, and if used carefully, will correctly set
distances. In fact, Dijkstra’s algorithm can be thought of simply as a sequence of $\tt update$’s.
We know this particular sequence doesn’t work with negative edges, but is there some other
sequence that does? To get a sense of the properties this sequence must possess, let’s pick a
node $t$ and look at the shortest path to it from $s$.
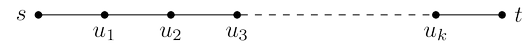
This path can have at most $|V | − 1$ edges (do you see why?). If the sequence of updates
performed includes $(s, u_1 )$, $(u_1 , u_2 )$, $(u_2 , u_3 ), \dots, (u_k , t)$, in that order (though not necessarily
consecutively), then by the first property the distance to $t$ will be correctly computed. It doesn’t
matter what other updates occur on these edges, or what happens in the rest of the graph,
because updates are safe.
But still, if we don’t know all the shortest paths beforehand, how can we be sure to update
the right edges in the right order? Here is an easy solution: simply update all the edges,
$|V | − 1$ times! The resulting $O(|V | \cdot |E|)$ procedure is called the Bellman-Ford algorithm and
is shown below together with an example run.

A note about implementation: for many graphs, the maximum number of edges in any
shortest path is substantially less than $|V | − 1$, with the result that fewer rounds of updates
are needed. Therefore, it makes sense to add an extra check to the shortest-path algorithm,
to make it terminate immediately after any round in which no update occurred.
Negative cycles
If the length of edge $(E, B)$ in the graph above were changed to $−4$, the graph would have a negative
cycle $A \rightarrow E \rightarrow B \rightarrow A$. In such situations, it doesn’t make sense to even ask about shortest
paths. There is a path of length $2$ from $A$ to $E$. But going round the cycle, there’s also a path
of length $1$, and going round multiple times, we find paths of lengths $0$, $−1$, $−2$, and so on.
The shortest-path problem is ill-posed in graphs with negative cycles. As might be
expected, our algorithm works only in the absence of such cycles. But where
did this assumption appear in the derivation of the algorithm? Well, it slipped in when we
asserted the existence of a shortest path from $s$ to $t$.
Fortunately, it is easy to automatically detect negative cycles and issue a warning. Such a
cycle would allow us to endlessly apply rounds of $\tt update$ operations, reducing $dist$ estimates
every time. So instead of stopping after $|V | − 1$ iterations, perform one extra round. There is
a negative cycle if and only if some dist value is reduced during this final round.
Source: Algorithms by Dasgupta, Papadimitriou, Vazirani. McGraw-Hill. 2006.